Gong Yong的Blog

一致性哈希

简介

传统的哈希表通常使用下面的方法将key映射到数组的索引（index）：

hash = hashFunc(key)
index = hash % arraySize

这种方法的不足之处是当arraySize发生改变后，所有的key都需要重新映射（remapped），因为索引的值是对arraySize求余运算获得的。

这种技术可以用于把应用程序的数据分散存储到多个数据库（注1）中，从而实现数据分区（data partition），只需要把key的哈希值跟数据库的个数进行求余运算，得到的结果就是存放这个key的数据库的序号，如下图所示：

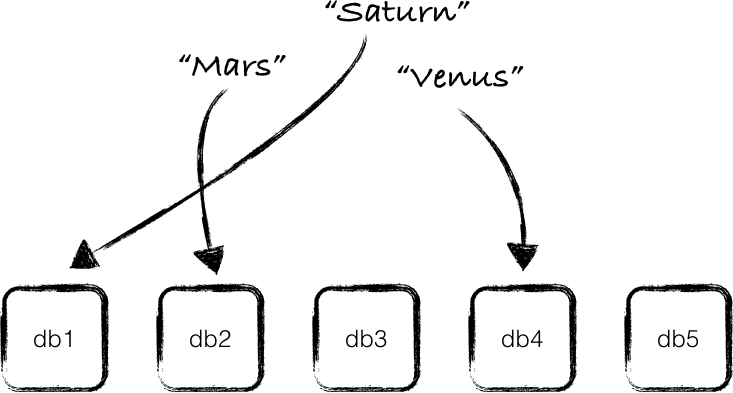
如果一个新数据库被添加到集群中，或者一个现有的数据库被移除出集群（或者是数据库服务器宕机），那所有的key都需要被重新映射，跟上面所说的哈希表的情况一样。假如你所要处理的数据非常多，你可以想象对所有的key进行重新映射将是一个非常耗时的工作，显然这很无聊。


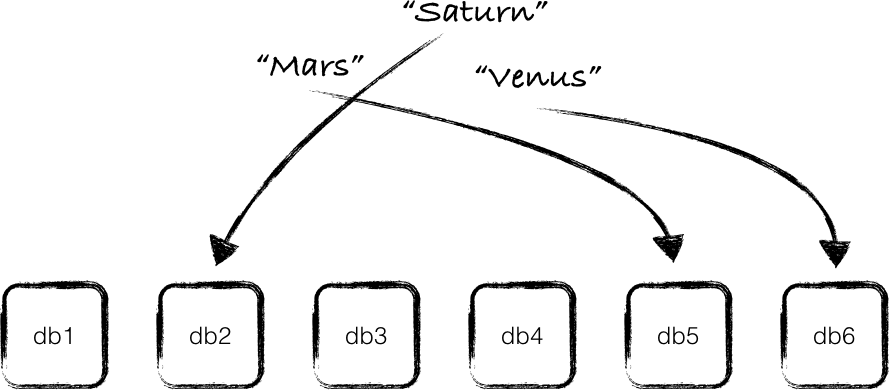
一致性哈希

一致性哈希就是用于解决这种问题的。首先，我们先看看函数 f 的输出的值的范围：

如果把输出的两端连起来就会形成一个环：

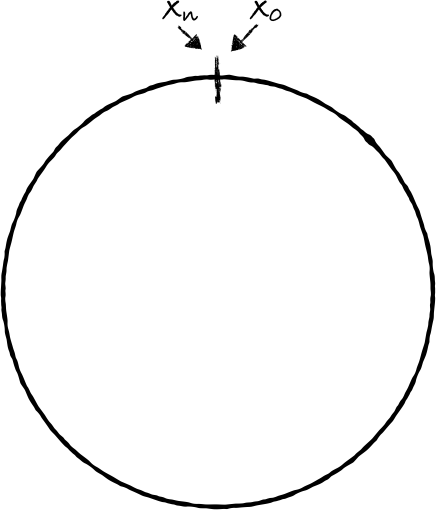
使用同样的函数 f ，我们把每个节点（node，可以理解成数据库服务器，key就是服务器的ip地址）映射到环上的一个点（a point）：

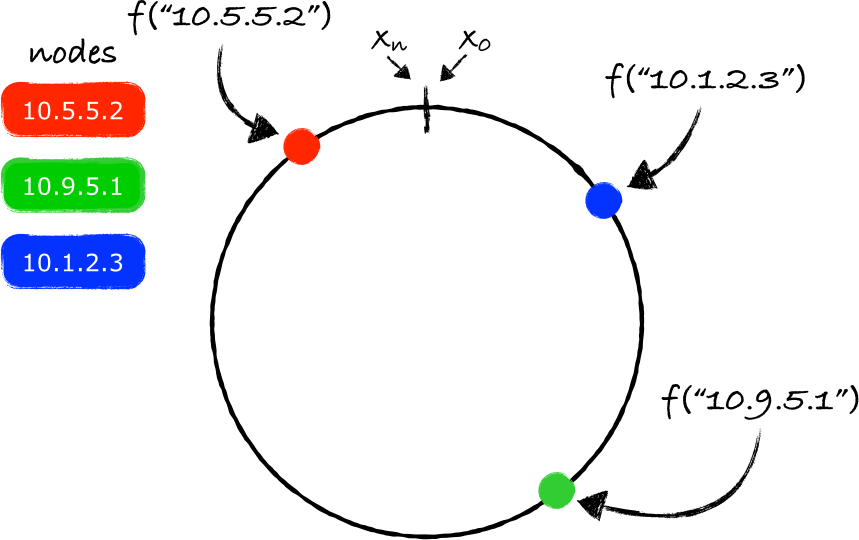
在这个环上两个节点之间的间隔就形成了一个分区（a partition）。如果我们对任何一个key使用同样的函数 f （注2），那么我们最终会得到这个key在环上的一个映射点（projection）：

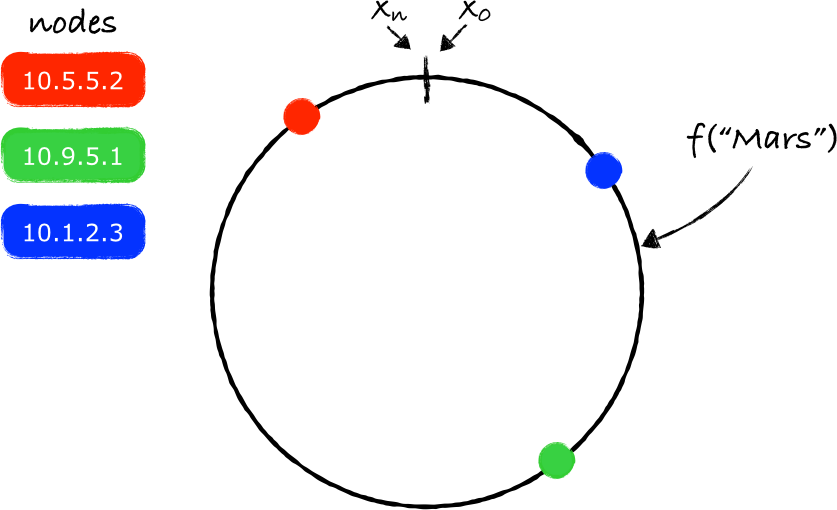
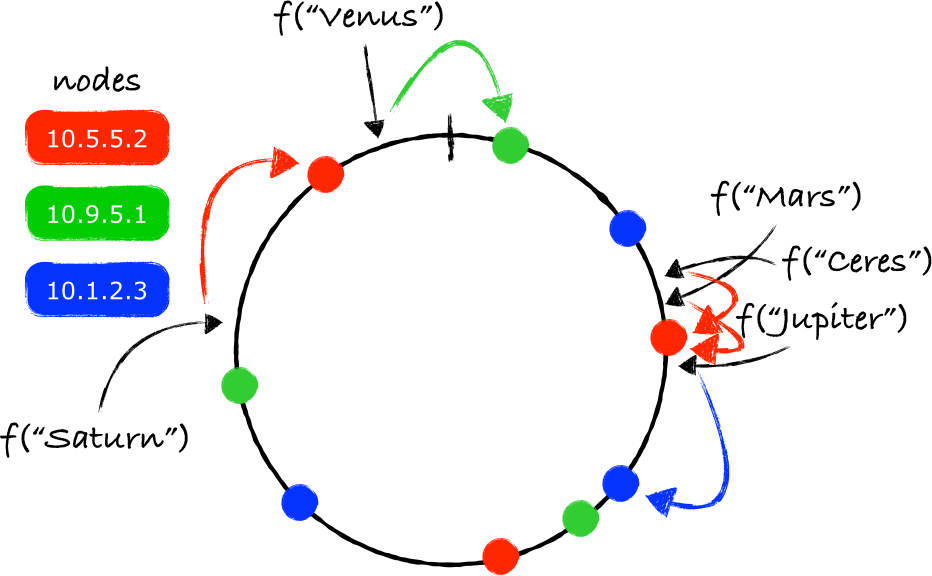
根据上面的理论，我们现在的任务是要确定存放key的服务器——我们从key对应的环上的映射点开始，沿着环做顺时针移动，碰到的第一个服务器节点就是负责存放key的服务器（注3）。

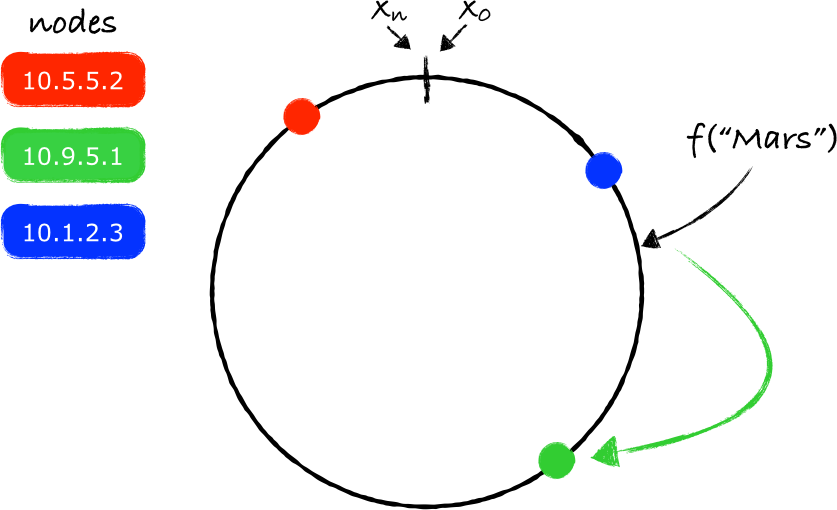
在上图所给出的示例中，"Mars"应该存放在服务器10.9.5.1上（绿色的节点）。同样的处理方法也可以用于其他的key：

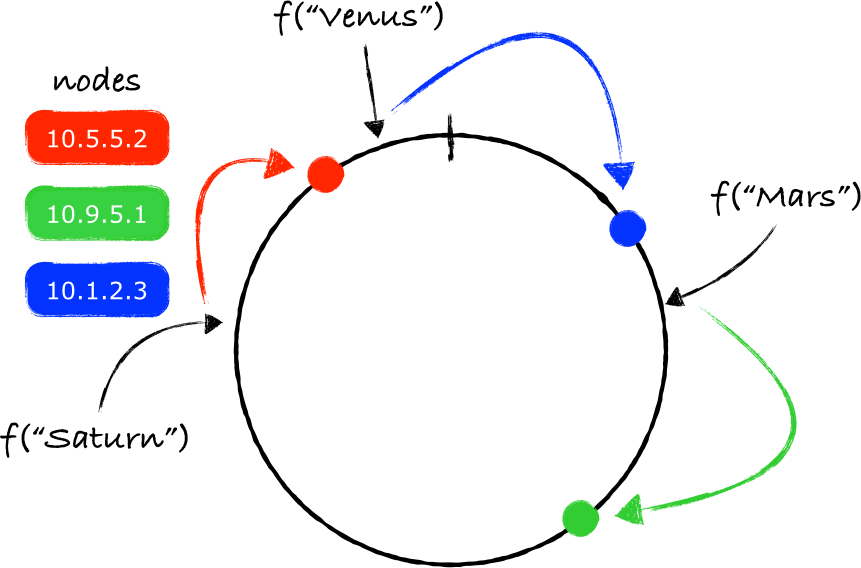
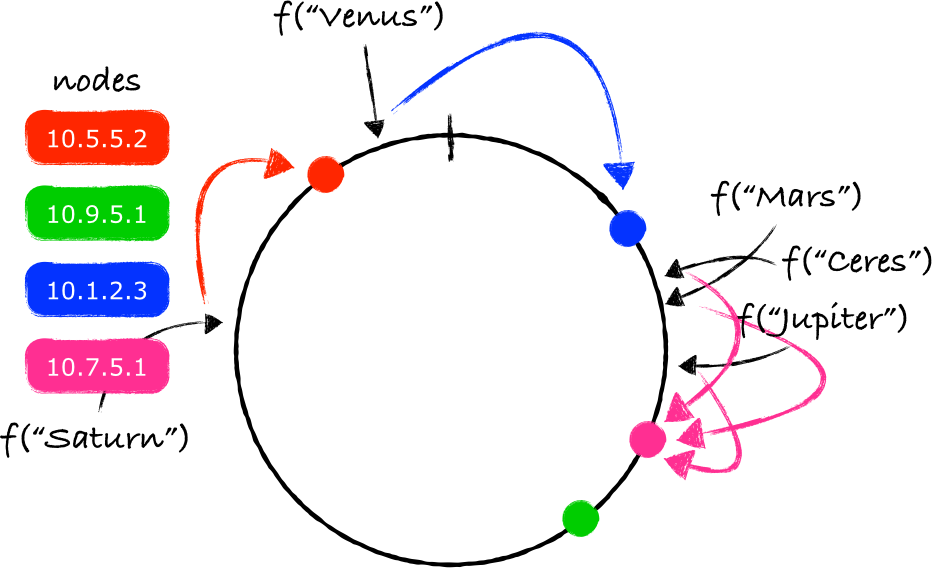
注意 f("Venus") 映射的点位于最后一个节点之后，但在函数 f 能返回的最大值之前。由于两个端点被连接起来了，所以沿着顺时针移动依旧可行，最终找到的节点就是10.1.2.3（蓝色的节点）。

在环上添加一个新节点并不意味着所有的key都需要重新映射。只有一部分key（注4）需要被重新映射到一个不同的节点上：

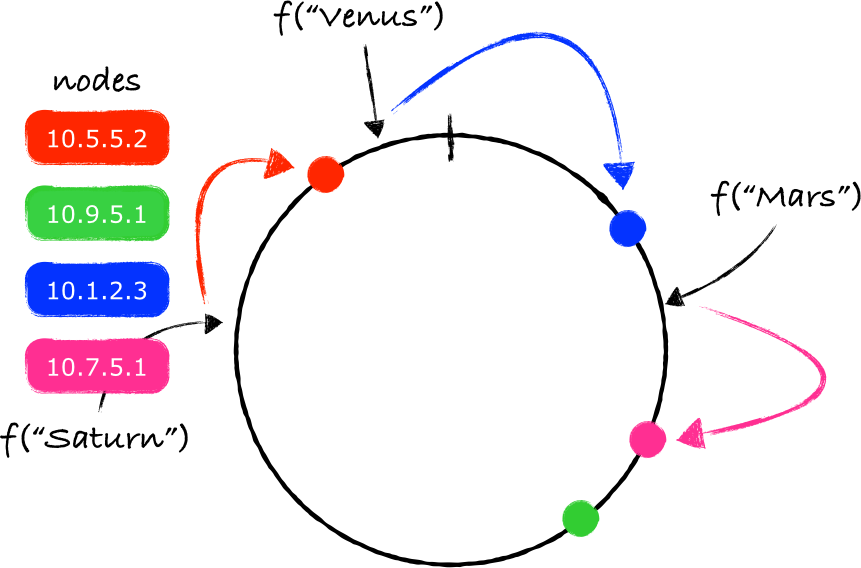
当一个节点被从环上移除，也只会有一部分key需要被重新映射：

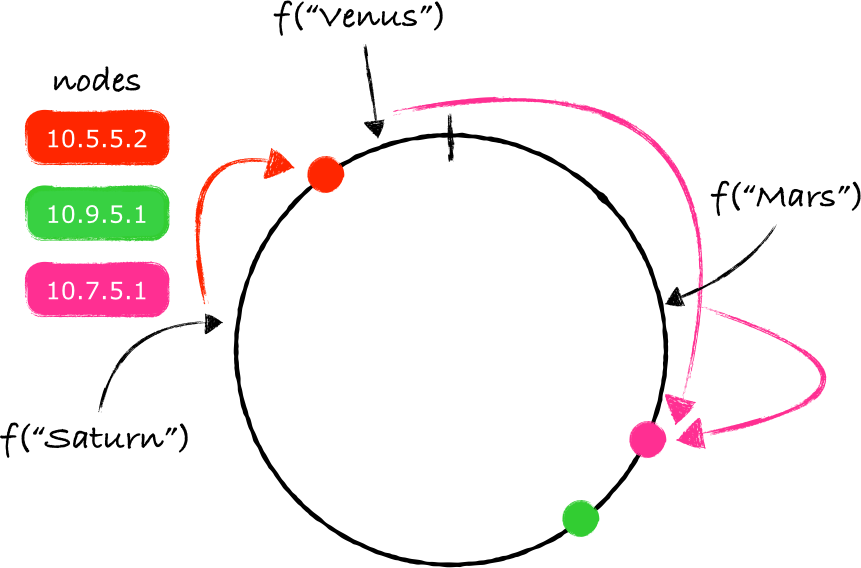
上面所介绍的算法就是一致性哈希的本质。这个想法是由Karger等人在1997的一篇论文中提到的 [1] 。所有节点被映射到一个环上，从而形成分区，之后再把key同样映射到环上，再沿着顺时针方向找到离key的映射点最近的节点，这个节点就是负责存储key的服务器节点。

使用了一致性哈希的系统有：Amazon's Dynamo [2] 、Riak [3] 、Akka [4] 和 Chord [5] 。

使用一致性哈希可以避免热点问题，只要函数 f 返回的哈希值足够均匀。所以即使多个看起来很相似的key，它们在环上的映射点也会完全不同，并且相距甚远，最终它们会被存放到不同的节点上。另外一个好处时当有新节点加入或从环上移除时，需要移动的key很容易处理，只是紧紧相邻的节点才会受到影响，对其他的节点则毫发无损。

使用一致性哈希的系统还可以使用其他技术来减轻环结构的改变所带来的不利影响。如果节点被用于存储数据，类似于本文开头的示例，系统可以在负责存储数据的原始节点N1之后的N个节点中复制N1中的数据。如果N1被从环上移除，紧挨着它的节点可能已经保存了N1的数据，这可以防止某个节点（这里是N1）的离开造成网络访问量的激增。这个技术也可以用于避免热点问题，因为对数据的请求既可以由N1来处理，也可以让节点N1后面的N个邻居节点中的一个来处理。

使用一致性哈希的系统通常使用一种哈希函数的输出范围来构建环结构，哈希函数可以是SHA-1或者SHA-2。SHA-1的输出范围是从0到2^160，SHA-2的输出范围各不相同，SHA-256是0到2^256，SHA-512是0到2^512等等。使用这些函数中的任何一个都会把节点映射到环上的一个随机位置。这样的得到的分区很可能不同的大小，换句话说就是每个节点所负责的数据量各不相同。这一特点的用处不大，不过这些哈希函数的输出范围都是固定的，所以整个环可以被预先分割为几个大小相等的分区，然后每个节点可以占有其中的几个分区，从而保证每个节点所处理的数据量基本相同。

另一个重要的技术是虚拟节点（virtual nodes）。

虚拟节点

上面的介绍的环的特点是环上的节点跟一个真实存在的物理节点进行一对一映射。这会引出一个问题，随机在环上放置节点（译注：添加节点）可能会导致节点间的数据分布不均匀。

当一个节点被从环上移除的时候，这个问题会变得更明显，此时所有由这个节点所处理的数据都要被转移到一个其他的节点上。

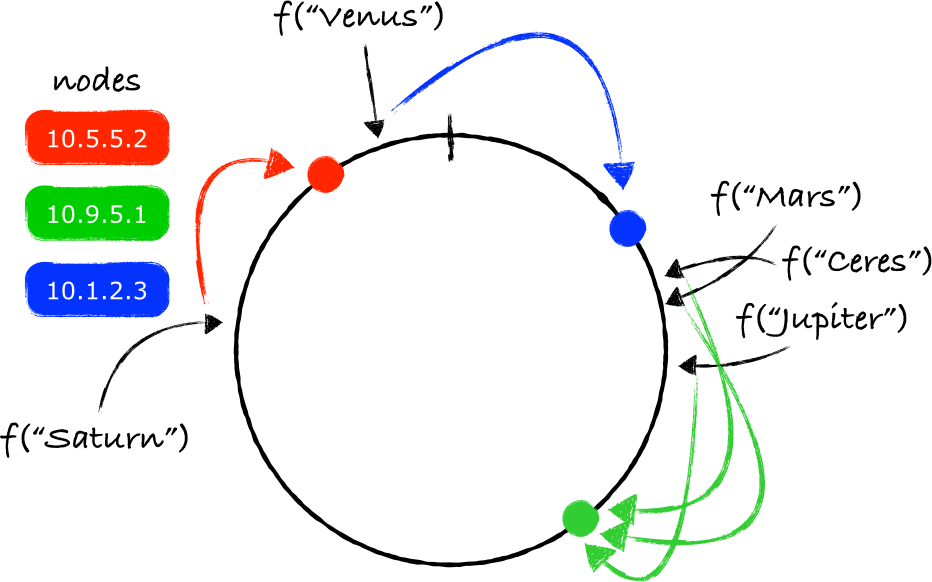
为了防止一个节点的移除导致另一个节点负载过大，同时为了让key的分布更加均匀，系统可以为物理节点和环上的节点建立一个不同的映射。除了本身存在的一对一的映射，系统还可以创建一些虚拟节点，并在物理节点和虚拟节点之间创建一个M对N的映射。

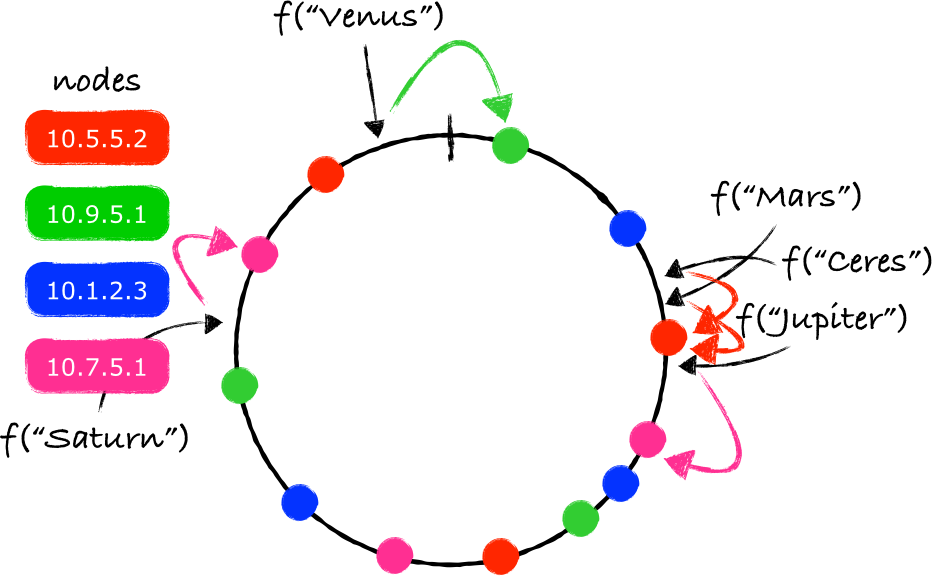
有了这些虚拟节点，每个物理节点将会负责环上的多个分区。当一个节点被移除，由这个节点处理的负载会被平均分配给环上剩余的其他节点。

类似地，当一个节点加入到环上，它会从环上其他的每个节点中接收数据量相同的部分数据。虚拟节点对于由资源各异的各种不同的节点组成的系统也会有帮助，这些资源包括CPU核心、RAM和磁盘空间等。对于这种节点各异的集群，虚拟节点的数量可以根据物理节点的特性来确定。

引用

注释


原文链接：http://blog.carlosgaldino.com/consistent-hashing.html